Deep Learning
看B站台湾大学教授李宏毅的深度学习课程的笔记
Deep Learning
基本概念
在监督学习中,数据集一开始可以粗略分为训练集和测试集。训练集是用于训练模型的数据集,往往已经打好了标签。测试集是模型处于应用阶段时真正处理的数据,所以对于模型训练是未知的。
用数据训练模型时,为减少过拟合的发生,使模型在测试集上也能表现出类似训练集上的性能,往往将训练集划分出一部分作为开发集(Dev),这部分开发集不参与模型训练,而只是用于检验训练出来的模型是否能够较好地应用于解决问题。
线性模型
model: \(\hat y=\omega*x + b\)
Training Loss(Error): \(loss = (\hat y - y)^2=(\omega * x - y)^2\)
Mean Square Error(MSE): \(cost = \frac{1}{N}\sum^N_{n=1}(\hat y_n-y_n)^2\)
穷举法
穷举\(\omega\)的值,取cost最小的\(\omega\)作为训练结果
MSE随着数据集规模的增大先减小后增大,转折点之前为欠拟合,转折点之后为过拟合。
梯度下降算法
- 利用函数的导数不断逼近极小值的方法。
- 只能求解局部最小值,不保证是全局最小值,是一种贪心算法
- 实际应用中往往没有很多局部最小值,更多的是鞍点
- 要对数据集所有数据进行处理,效率较低
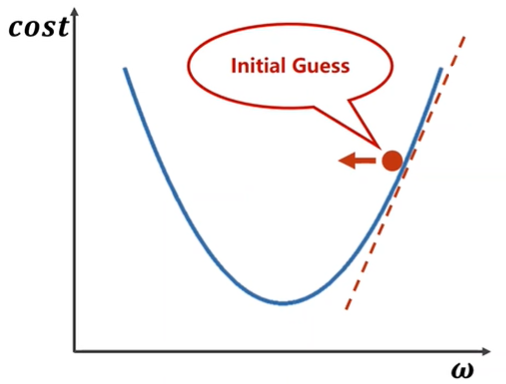
\(\omega = \omega - \alpha\frac{\partial cost}{\partial\omega}\),其中\(\alpha\)为学习率。
不断迭代\(\omega\)直到它收敛(cost收敛)。
如果发现cost没有收敛到一定的值而是发散,则本次训练失败,很可能是由学习率太大引起。
为了观察训练数据的趋势,将迭代过程中得到的cost值记为\(C_0, C_1, C_2,...\),对其作一定的平滑处理,\(C_0'=C_0, C_i'=\beta C_i + (1-\beta)C_{i-1}'\)
随机梯度下降(Stochastic Gradient Descent)
不取cost,而是通过随机取一个样本的loss引入一个随机的噪声,这样能够克服鞍点,且运算效率较高。
对于\(\hat y_n=x_n\cdot \omega\),有下图

批量梯度下降(mini-batch)
将样本均分为若干组,每组并行用梯度下降算法,组间使用随机梯度下降算法,效率较高又能较稳定地收敛。
计算图(Computational Graph)
当参数较多时,样本之间的关系往往呈现非常复杂的结构。
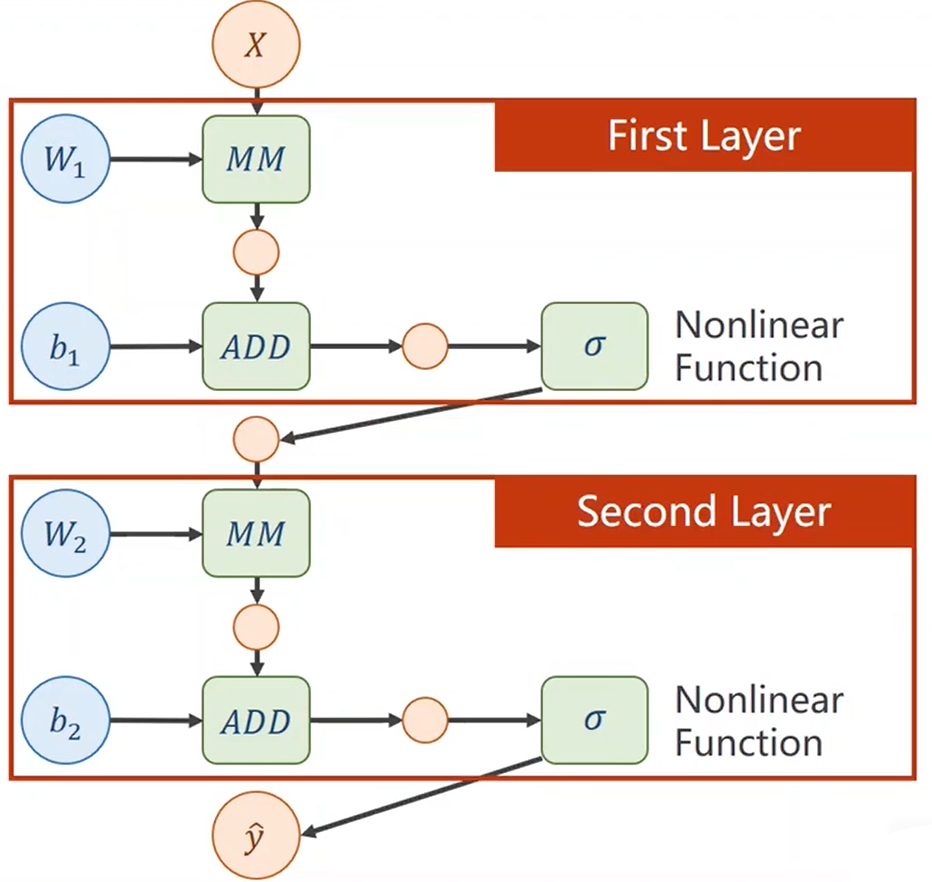
这时候往往用矩阵表示相邻层级间的函数关系。
如果只是简单地用一个变换矩阵和一个bias从上一层级得到下一层级,则最后得到的层级一定可以从第一层级直接变换得到。 \[ \hat y=W_2(W_1\cdot X+b_1)+b_2=W_2W_1X+W_2b_1+b_2=WX+b\tag 1 \] 那么多层级就变得没有了意义。
所以需要引入一个非线性的函数\(\sigma\),\(\hat y_1 = W_1\cdot X + b_1 + \sigma\)。
对于(1)式,可以绘制出它的计算图如下。
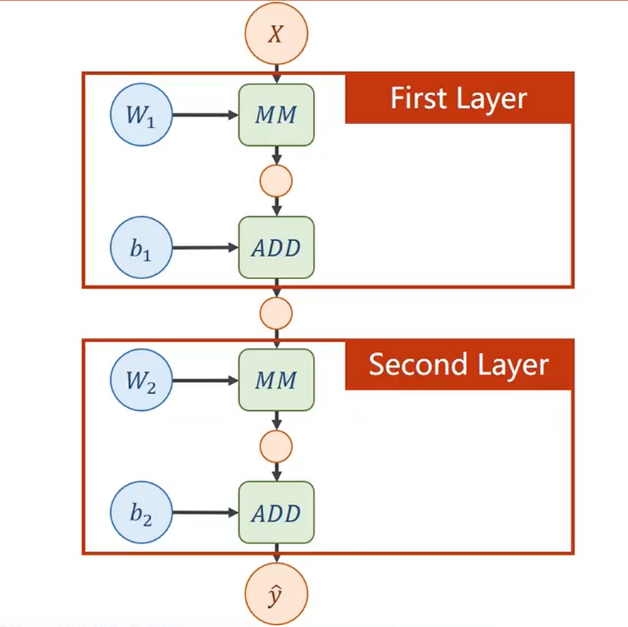
更准确地,应绘制成下图。
计算图的梯度运算
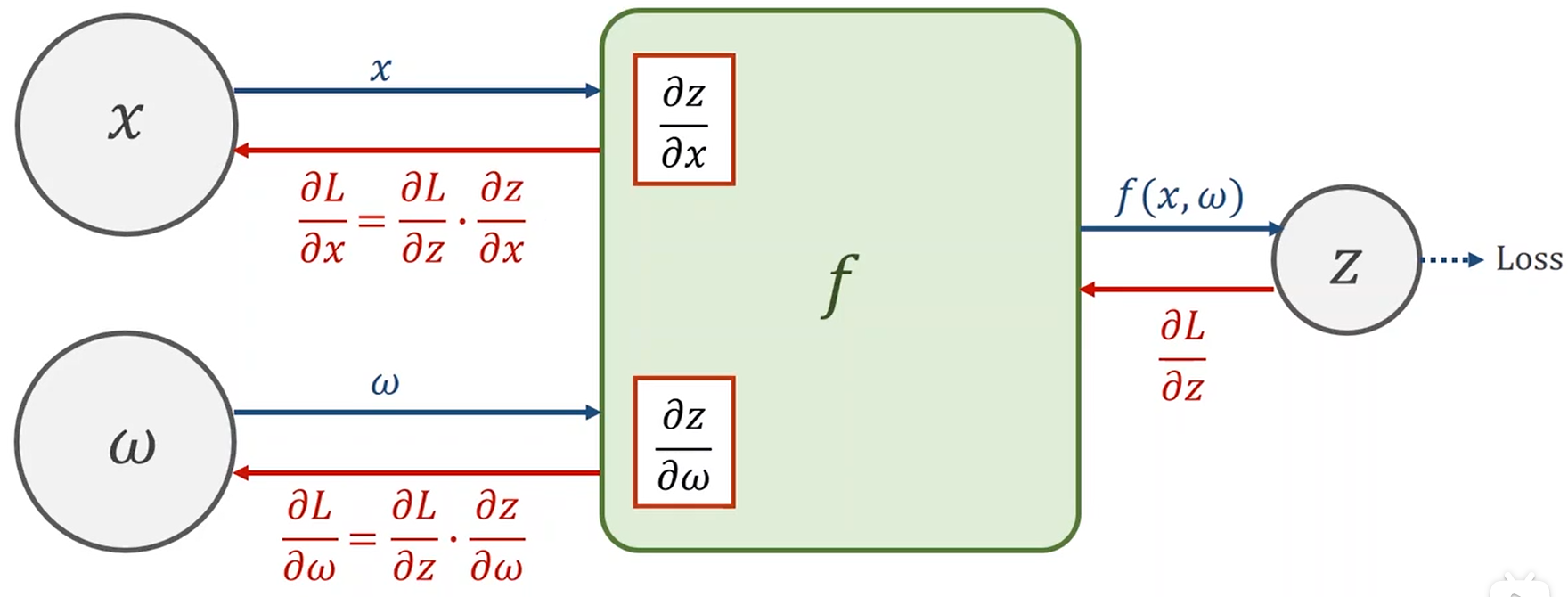
前馈时得到\(\frac {\partial z}{\partial x}\)和\(\frac{\partial z}{\partial \omega}\),后馈时根据计算好的\(\frac {\partial z}{\partial x}\)和\(\frac{\partial z}{\partial \omega}\),利用链式法则得到\(\frac{\partial L}{\partial x}\)和\(\frac{\partial L}{\partial \omega}\),这就是梯度运算时需要用到的梯度。
PyTorch
- torch中基本的数据类型为Tensor,在运用tensor类进行计算时往往会构建计算图,它包含data和grad,它们也都是Tensor类型的
- 记一个Tensor类的变量为tensor,则有
tensor = torch.Tensor([预估计值])tensor.data返回的也是一个Tensor类的值,但不会构建运算图,tensor.Item()返回python标准数据类型- 默认情况下tensor不含梯度,但可以通过
tensor.requires_grad = True使其包含梯度 - tensor与python标准类型的数据的运算返回结果依然为Tensor类
tensor.zero_()实现清零,训练时梯度使用一次后往往要清零,因为要重新计算。- 调用一个含Tensor类的方法相当于完成了一次前馈计算,通过
tensor.backward()完成后馈计算,更新我们需要的梯度