GAMES202笔记
Real-Time High Quality Rendering
实时:速度快于30FPS,对于VR、AR要求90FPS
interactive:像幻灯片一样,比较慢,但能交互
CG Basics
Graphics Pipeline
flowchart TD
id1(Application)
id2[Vertex Processing]
id3[Triangle Processing]
id4[Rasterization]
id5[Fragment Processing]
id6[Framebuffer Operations]
id7(display)
id1-->id2-->|Vertex Stream|id3-->|Triangle Stream|id4-->|Fragment Stream|id5-->|Shaded Fragments|id6-->id7
OpenGL
- Place objects/models
- Model specification
- Model transformation
- send object to GPU as a Vertex buffer object(VBO)
- Set up an easel
- View transformation
- Create / use a framebuffer
- Set camera, e.g. gluPerspective
- Attach a canvas to the easel
- OpenGL的一个优点:multiple render target(BRT)
- 一个rendering pass指定一个framebuffer,但可以有多个textures作为输出
- framebuffer直接绘制到屏幕容易出现画面撕裂的效果,打开垂直同步其实就是不直接绘制,双重缓冲、三重缓冲技术
- Paint to the canvas
- 顶点着色器、片元着色器
- 深度测试
OpenGL Shading Language (GLSL)
调试shader
Nsight Graphics(跨平台,但仅支持NVIDIA GPUs)
RenderDoc(跨平台,不限制GPU)
用颜色作为输出print出来
The Rendering Equation
In real-time rendering(RTR)
- Visibility is often explicitly considered
- BRDF is often considered together with cosine term
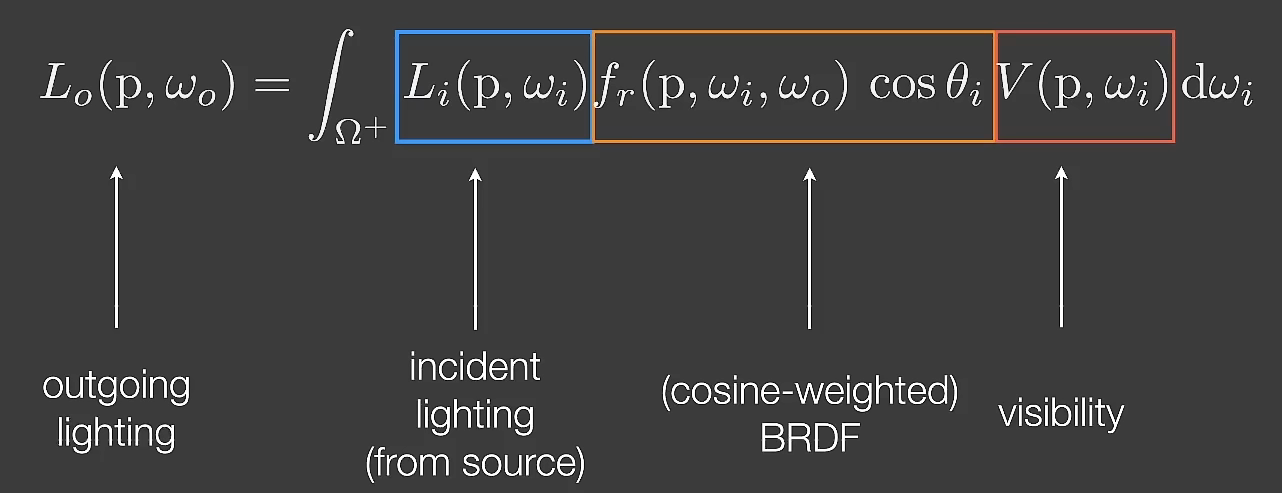
实时渲染中通常只考虑光线弹射一次
Real-Time Shadows
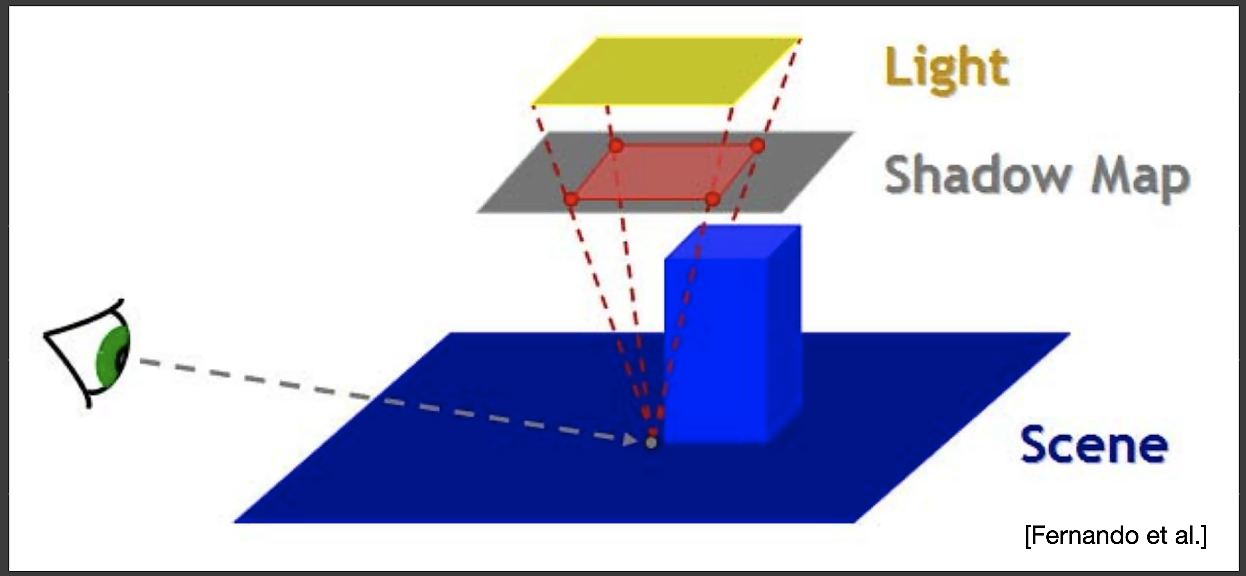
Recap: shadow mapping
- A 2-Pass Algorithm
- 先从光源发射光线,得到Shadow Map(SM)
- 从相机发射光源,根据SM
- An image-space algorithm
- Pro: 不需要知道场景的几何
- Con:自遮挡和走样
先从光源出发,得到各个角度能照到的点的深度作为shadow map。再从相机出发,根据相机照到的点检测是否在shadow map中决定是否有阴影。
shadow mapping存在的问题
光线与阴影所投平面不垂直时,由于shadow map得到的每个点的深度是不连续的,会出现自遮挡的问题

为解决该问题,可以引入一个和光线与平面夹角有关的误差允许bias,但这样又会造成detached shadow.

工业界往往通过调整bias达到既没有自遮挡又没有detached shadow的效果。
其他的解决方案:Second-depth shadow mapping
- 在shadow map中记录最近和次近的点的深度,通过与最近和次近的点的中点的深度的比较决定是否有阴影
- 开销略大,且要求不能有没厚度的物体,所以基本没有被使用
The math behind shadow mapping
\[ \int_{\Omega}f(x)g(x)dx\approx\frac{\int_\Omega f(x)dx}{\int_\Omega dx}\cdot\int_\Omega g(x)dx\tag {small support or smooth integrand} \]
small support: 积分区间很小
smooth integrand: 被积函数积分范围内变化不大
由此,可以得到渲染方程 \[ \begin{align} L_o(p, \omega_o)&=\int_{\Omega+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)cos\theta_iV(p,\omega_i)d\omega_i\\ &\approx\frac{\int_{\Omega+}V(p,\omega_i)d\omega_i}{\int_{\Omega+}d\omega_i}\cdot\int_{\Omega+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)cos\theta_id\omega_o \end{align} \] 约等式右边的第一项是Visibility,第二项是Shading,这其实就是shadow map做的事。
什么时候近似准确
- Small support(积分限小): point / directional lighting
- Smooth integrand(变化小): diffuse bsdf / constant radiance area lighting
- 两个满足一个就够了
Percentage closer soft shadows(PCSS)
Percentage Closer Filtering(PCF)
- 最初是用于抗锯齿
- 后发现可以用于软阴影
将着色点相对light的深度和着色点在shadow map上周围的一系列点(比如7*7,filter size)的深度进行比较,取平均得到visibility。注意不是对shadowmap做模糊处理。
filter size越大,阴影越软,反之越硬。
可以通过调节不同地方的filter size获得阴影软硬的变化,这样也就得到了PCSS。物体里阴影投射面越近的地方阴影越硬,越远越软。
PCSS原理
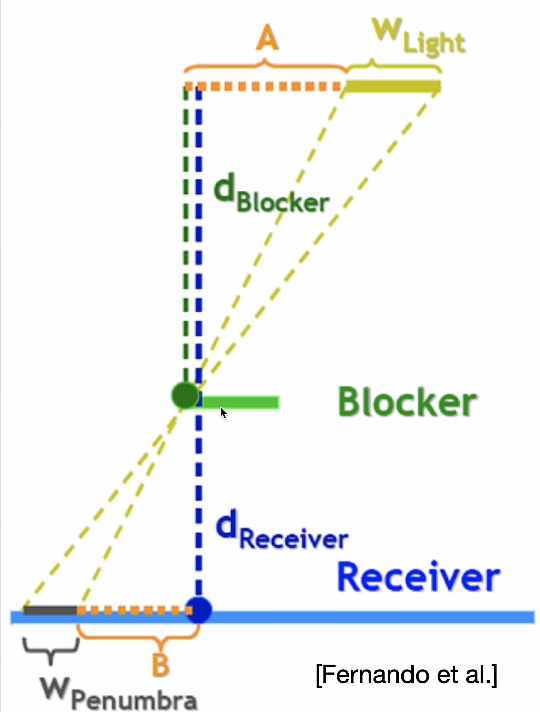
\(w_{Penumbra}\)实际上就是软阴影。
由相似可以得到 \[ w_{Penumbra}=(d_{Receiver}-d_{Blocker})\cdot w_{Light} / d_{Blocker} \]
具体实现
面光源取中心生成shadow map
- Blocker search: getting the average blocker depth in a certain
region
- region可采用常数或启发式
- 启发式的region为着色点与光源的连线在shadow map(近平面)上的范围
- Penumbra estimation: use the average blocker depth to determine filter size
- Percentage Closer Filtering
在filter size大的时候开销很大,可以采用稀疏采样再图像降噪的方法来降低开销。
Variance soft shadow mapping
在temperal denoising方法提出后使用的没有PCSS多了
加速PCF
Shadow Mapping实际上就是得出shading point比filter的box里的百分之几的点近,如果知道分布,那么就可以快速得出这一点。
可以使用mean和variance来描述一个分布
- Mean
- Hardware MipMaping(只能求方形的mean,不能对任意矩形区域求mean,但很快)
- Summed Area Tables(SAT,会慢一些)
- Variance
- \(Var(X)=E(X^2)-E^2(X)\)
- 需要额外的\(depth^2\)的shadow map,根据这个shadow map生成mipmap或SAT
- 可以将\(depth\)作为一个颜色通道,\(depth^2\)作为另一个颜色通道
- \(Var(X)=E(X^2)-E^2(X)\)
- 计算CDF
- 求数值解慢
- 查表(Error Function,在C++中是e2f)需要大量空间
- 用切比雪夫不等式来近似:\(P(x>t)\le\frac{\sigma^2}{\sigma^2+(t-\mu)^2}\)(\(t>\mu\),对分布的类型没有要求,但是正态分布时非常近似)
加速Blocker Search
Blocker Search求的是一个块状区域内遮挡物的深度的均值\(z_{occ}\),记shading point的深度为t,块状区域内非遮挡物的深度的均值为\(z_{unocc}\),则有 \[ \frac{N_1}{N}z_{unocc}+\frac{N_2}{N}z_{occ}=z_{Avg} \] 用切比雪夫不等式近似,\(\frac{N_1}{N}=P(x>t),\frac{N2}{N}=1-P(x>t)\),大胆假设\(z_{unocc}=t\),这样就能解出\(z_{occ}\)
MIPMAP and Summed-Area Variance Shadow Maps
MIPMAP可能需要双线性插值甚至三线性插值,会不准。
SAT是记录从(0, 0)到(i, j)的矩形元素的和(前缀和思想的二维应用)。先按行并行求,再按列并行加起来。
Moment shadow mapping
VSSM只用了\(z\)和\(z^2\)来表示分布,所以对于正态分布效果比较好,对其他分布则由于不够近似容易出现问题,会出现一些区域过黑(可以接受),一些区域过亮(light leaking,不可接受)。MSM引入了更高阶的矩(moment)来实现更好地表述分布。通常到\(z^4\)就能取得很好的效果。
但是从四阶矩重建出CDF开销比较大。
Distance field soft shadows
Distance Function: At any point, giving the minimum distance(could be signed distance) to the closest location on an object. 即空间中一个点到所有物体的最近距离。
SDF:signed。可以定位物体内部的距离为负数,外部为正数。人们通常情况不管是否signed都称之为SDF。
blend
SDF可以用于blend物体边界。直接对两张有明显边界的图进行线性插值显然无法得到边界移动的中间结果。

但是SDF就可以很好地实现这一点。
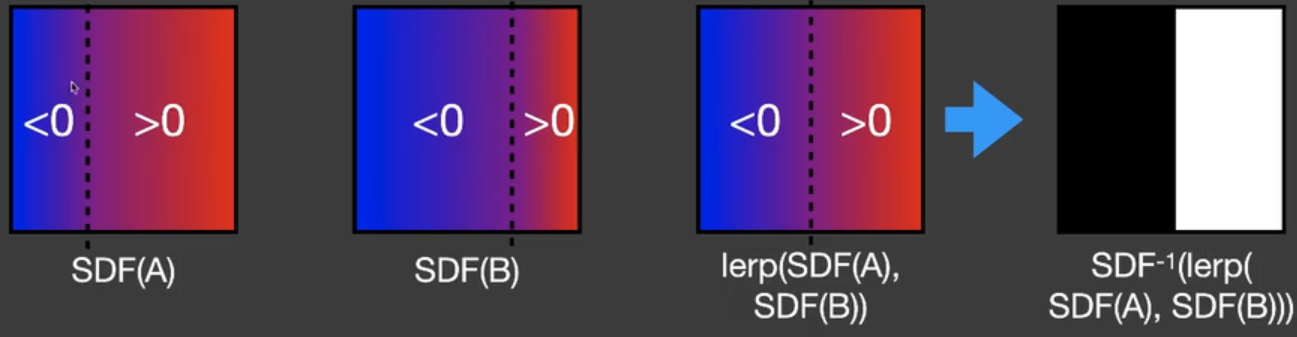
进而实现这样的变化。

Usage
Ray Marching
SDF的值可以看作a safe distance around。因此,对于在p点的光线,可以前进\(SDF(p)\)的距离,不断迭代,直到到达物体。

determine the approx percentage of occlusion
SDF的值可以看作a safe angle seen from the eye。

着色点的safe angle越小,表明被遮挡得越厉害,即less visibility。
safe angle的计算:在ray marching的时候计算各个点对应的角度,取最小的角度,表达式显而易见为\(arcsin(\frac{SDF(p)}{d_{travel}})\)。但是反三角函数的计算比较复杂,实际上可以直接用反三角函数前的值来表示。即\(min\{\frac{kSDF(p)}{|p-o|}, 1.0\}\),o为光线出发的地方。这里的k实际上可以看作对阴影软硬的控制的系数,k越大阴影越硬。
- Pros
- Fast(不考虑DF的计算)
- High quality
- Cons
- Need precomputation
- Need heavy storage
- 对于物体形变需要重新计算SDF
- Artifact
Real-time Environment Mapping
认为光照来自无限远。
主流的两种存储方式:Spherical map和Cube map
Shading from Environment Lighting
由于上述的存储方式,环境光照又称为Image-Based Lighting(IBL)
使用它进行着色,在不考虑visibility的情况下 \[ L_o(p, \omega_o)=\int_{\Omega+}L_i(p, \omega_i)f_r(p, w_i, w_o)cos\theta_id\omega_i \] \(\Omega+\)表示上半球,和着色点的法线方向相关。
为解这个方程,直观的想法是使用蒙特卡洛积分,但是需要大量采样,开销很大。
在实时渲染中,往往不使用sampling。但是现在很多降噪方法的提出使得这一点变得不那么绝对。
BRDF往往要么是glossy的,要么是diffuse的。glossy意味着small support,diffuse意味着smooth,
可以联想到这个近似式 \[ \int_\Omega f(x)g(x)dx\approx\frac{\int_{\Omega_G}f(x)dx}{\int_{\Omega_G}dx}\int_\Omega g(x)dx \] 那么渲染方程就可以写作 \[ L_o(p, \omega_o)\approx\frac{\int_{\Omega_{f_r}}L_i(p, \omega_i)d\omega_i}{\int_{\Omega_{f_r}}d\omega_i}\int_{\Omega+}f_r(p,\omega_i,\omega_o)cos\theta_id\omega_i \] 右边的第一项其实就是对环境光做滤波。可以prefilter environment light,得到一组不同滤波核滤波的环境光。在着色时只需要查询着色点反射方向的prefiltered environment lighting即可。
实际上我们可以发现,原本的蒙特卡洛积分是在反射方向附近进行采样再加权平均,现在的则是预先filter再直接取值,两者非常近似。
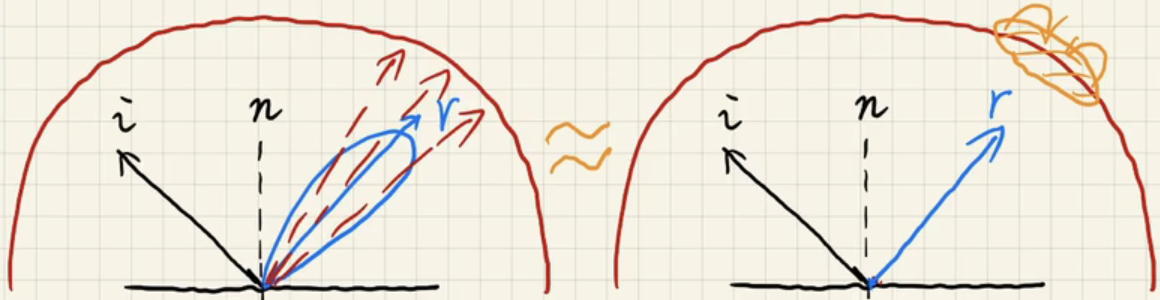
对于右边的第二项,核心思想是预计算,但是直接预计算的话维度很大,需要大量的存储空间。
这里我们使用Microfacet模型,F为菲涅尔项 \[ \begin{align} \int_{\Omega+}f_rcos\theta_id\omega_i&=\int_{\Omega+}\frac{f_r(p,\omega_i,\omega_o)}{F}Fcos\theta_id\omega_i\\ &\approx\int_{\Omega+}\frac{f_r}{F}(R_0+(1-R_0)(1-cos\theta)^5)cos\theta_id\omega_i(\text{Schlick's approximation})\\ &=R_0\int_{\Omega+}\frac{f_r}{F}(1-(1-cos\theta)^5)cos\theta_id\omega_i+\\ &\int_{\Omega+}\frac{f_r}{F}(1-cos\theta)^5cos\theta_id\omega_i \end{align} \] 而\(f_r(i,o)=\frac{F(i,h)G(i,o,h)D(h)}{4(n,i)(n,o)}\),\(\frac{f_r}{F}=\frac{G(i,o,h)D(h)}{4(n,i)(n,o)}\),因为不考虑shadow,所以忽略G项(shadowing-masking term),此时只和D和\(\theta\)有关。\(D(h)=\frac{e^{-\frac{tan^2\theta_h}{\alpha^2}}}{\pi\alpha^2cos^4\theta_h}\),\(\theta_h\)可以转化为\(\theta\)的表达式,所以最终只和\(\alpha\)(roughness)和\(cos\theta\)有关,所以只需要预计算一个二维的表,作为一个texture。这个texture为LUT。
这种将乘积的积分(求和)拆开先求积分(求和)再求乘积的方法被称为Split Sum Approximation。
Shadow from Environment Lighting
很难实现,通常工业界的做法是根据最强的光源决定阴影,或者用Ambient Occlusion。
Background knowledge
Frequency and filtering
Any product integral can be considered as filtering \[ \int_\Omega f(x)g(x)dx \] The frequency of the integral is the lowest of any individual's.
Basis functions
A set of functions that can be used to represent other functions in general \[ f(x)=\sum_i c_i\cdot B_i(x) \]
Real-time environment lighting
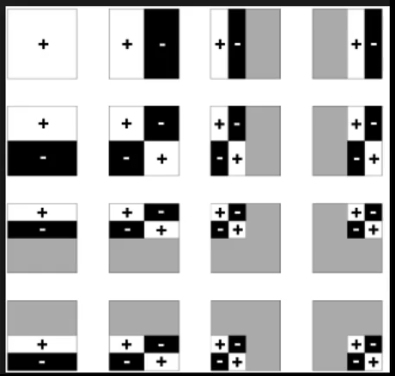
Spherical Harmonics(SH)
A set of 2D basis functions \(B_i(\omega)\) defined on the sphere.
可视化如图

给定一个\(\omega\),会与一个基函数有且只有一个交点,交点处的颜色即表示函数值的大小。
\(l\)是SH的阶数,第\(l\)阶SH有\(2l + 1\)个基函数,前\(l\)阶有\((l+1)^2\)个基函数。
SH使用时往往取前三阶。
越高阶的SH表示越高频率的信息,所以SH往往适用于低频信息。
基函数的系数的求解称为投影,可以通过下式得到 \[ c_i=\int_\Omega f(\omega)B_i(\omega)d\omega \] \(B_i(\omega)\)由勒让德多项式(Legendre polynomial)得到。
Prefiltered environment lighting
Diffuse的BRDF往往只有低频信息,所以基本只有前三阶(l=0,1,2)的系数非零。
Rendering Equation中\(L*fr*d\omega_i\)可以将\(f_r\)看作低通滤波(frequency of the integral is the lowest of any individual's),所以实际上L也没必要含高频信息。
对于任何光照,只要brdf是diffuse的,那么用前三阶作为光照,平均误差不超过3%。
Precomputed Radiance Transfer(PRT)
把Rendering Equation \[ L(o)=\int_\Omega L(i)V(i)\rho(i,o)max(0,n\cdot i)di \] 中的\(L(i)\)看作lighting,\(V(i)\rho(i,o)max(0,n\cdot i)\)看作light transport,可以发现lighting仅与\(i\)有关,是一个球面函数,light transport的变量也只有\(i\),也是一个球面函数。
\(L(i)\approx\sum l_j B_j(i)\)
考虑在场景中只有光照可以发生变化的情况,我们可以预计算light transport。
- Pro:可以方便地切换环境光,能够快速地处理光源的旋转,由于保留了V项,能够产生阴影
- Con:场景中的物体不能移动
Diffuse case
\[ \begin{align} L(o)&=\rho\int_\Omega L(i)V(i)max(0,n\cdot i)di\\ &\approx \rho\sum l_j\int_\Omega B_j(i)V(i)max(0, n\cdot i)di \end{align} \]
在实时渲染中,往往认为积分和求和顺序总是可交换(除了differentiable rendering)
上式的积分可以预计算,于是得到 \[ L(o)\approx\rho\sum l_jT_j \] 其中\(T_i\approx\int_\Omega B_j(i)V(i)max(0,n\cdot i)di\)
可以看到,积分最终变成了两个函数在同一组基函数上的投影的乘积,即点乘。
另一种思路 \[ L(\omega_i)\approx\sum_p c_pB_p(\omega_i)\\ T(\omega_i)\approx\rho\sum_q c_qB_q(\omega_i)\\ \begin{align} L_o(p,\omega_o)&=\int_{\Omega+}L(\omega_i)T(\omega_i)d\omega_i\\ &=\rho\sum_p\sum_qc_pc_q\int_{\Omega+}B_p(\omega_i)B_q(\omega_i)d\omega_i\\ &=\rho\sum l_jT_j(由正交性得) \end{align} \]
如果我们将上面\(T_j\)的式子看作渲染方程,\(B_j\)则相当于光照,\(T_j\)实际上就是着色点在\(B_j\)光照下的颜色。
Basis functions
采用SH作为basic function
SH的性质
- orthonormal
- \(\int_\Omega B_j(i)\cdot B_k(i)di=1\text{ if (j=k)}\)
- \(\int_\Omega B_j(i)\cdot B_k(i)di=0\text{ if (j}\ne\text{k)}\)
- simple projection/reconstruction
- simple rotation
- 当光源发生旋转时,就是对\(\sum l_j B_j(i)\)进行旋转,可以看作对各个\(B_j\)进行旋转,而SH中\(B_j\)旋转后的结果可以用同阶的SH的线性组合表示
- simple convolution
- few basis functions: low freqs
Glossy case
\[ \begin{align} L(o)&=\int_\Omega L(i)V(i)\rho(i,o)max(0,n\cdot i)di\\ &\approx\sum l_jT_j(o) \end{align} \]
在diffuse中,\(L\)是一个值,light transport预计算得到向量\([T_1,T2,...T_n]\)。
而在diffuse中,\(L(o)\)是一个向量,light transport预计算得到矩阵,\(L(o)\)约等于light的系数向量和transport系数矩阵的乘。
More Basis Functions
Wavelet(小波)
定义在图像块上,每个基函数的定义域不一定相同,(灰色为非定义域内)
Wavelet可以保留各个频率的信息。
每次对图像进行Wavelet transform,仅会有很少的基函数的系数非零,通过这个进行数据压缩,是一种非线性的近似。
由于Wavelet定义在图像块上,人们往往使用cubemap表示环境光而不是sphere,对cubemap的每张图分别进行Wavelet Transform。
Wavelet Transform
- 将高频信息留在右上、左下、右下,稍微低频的留在左上角,再对左上角递归做这样的操作。


JPEG就使用了一种类似小波变换的离散余弦变换DCT
小波变换一个比较大的缺点就是不支持旋转。
Real-time Global Illumination(in 3D)
在实时渲染中,全局光照往往只要求one bounce indirect illumination
Reflective Shadow Maps(RSM)
主要思路是将被直接光照照亮的表面作为新的次级光源,用来照亮其他点。
- 用shadow map可以获得直接被光源照亮的点
- shadow map上的每一个像素都是一个小的surface patch,可以作为面光源
- 渲染时只知道次级光源朝相机的radiance,但不知道朝被间接照亮的物体表面的radiance
- 假设所有reflector都是diffuse的,于是朝被间接照亮的物体表面的radiance等于朝相机的radiance(对接受物没有要求)
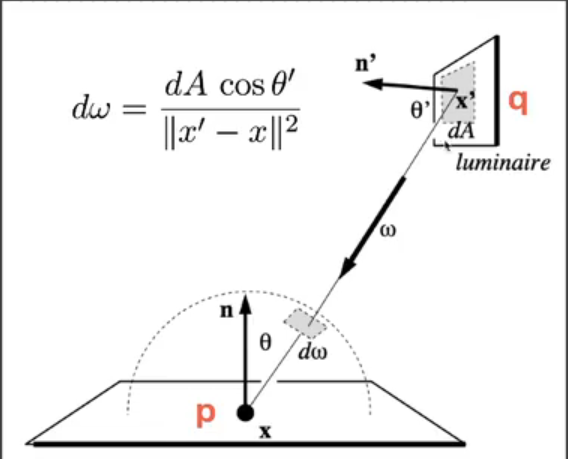 \[
\begin{align}
L_o(p,\omega_o)&=\int_{\Omega_{patch}}Li(p,\omega_i)V(p,\omega_i)f_{r_p}(p,\omega_i,\omega_o)cos\theta_i
d\omega_i\\
&=\int_{A_{patch}}L_i(q\rightarrow
p)V(p,\omega_i)f_{r_p}(p,q\rightarrow p,\omega_o)\frac{cos\theta_p
cos\theta_q}{||q-p||^2}dA
\end{align}
\] 对于diffuse的reflect,\(f_{r_q}=\frac{\rho}{\pi}\),\(\rho\)为albedo,根据BRDF的定义,有\(L_i=f_{r_q}\cdot
\frac{\Phi}{dA}\),其中\(\Phi\)是incident flux,由光源决定。
\[
\begin{align}
L_o(p,\omega_o)&=\int_{\Omega_{patch}}Li(p,\omega_i)V(p,\omega_i)f_{r_p}(p,\omega_i,\omega_o)cos\theta_i
d\omega_i\\
&=\int_{A_{patch}}L_i(q\rightarrow
p)V(p,\omega_i)f_{r_p}(p,q\rightarrow p,\omega_o)\frac{cos\theta_p
cos\theta_q}{||q-p||^2}dA
\end{align}
\] 对于diffuse的reflect,\(f_{r_q}=\frac{\rho}{\pi}\),\(\rho\)为albedo,根据BRDF的定义,有\(L_i=f_{r_q}\cdot
\frac{\Phi}{dA}\),其中\(\Phi\)是incident flux,由光源决定。
由此可以得到q给x点的Irradiance,\(E_q(x,n)=L_i(q\rightarrow p)\cdot\frac{cos\theta_p cos\theta_q}{||q-p||^2}dA =\Phi_q\frac{max\{0,<n_q|x-x_q>\}max\{0,<n|x_q-x>\}}{||x-x_q||^4}\)
遮挡问题由于没法求解,所以visibility直接不算
对于每一个shading point,都需要求shadow map上的所有像素的贡献,这样很明显计算量太大了,而且有一些像素可以简单地判断出没有贡献。为了实现判断,需要在shadow map上记录一些额外的信息,除了深度以外,还包括世界坐标、法向量、flux。可以通过着色点和secondary light连线的方向和法线的夹角判断简单的遮挡关系。
为了减少计算量,采用和PCSS类似的方法,仅对部分点进行采样。考虑到彼此之间越近的reflector和receiver贡献越大,假设深度图上越近且深度接近的点的世界坐标也足够近,仅对这些点进行采样,这样子计算量就不再是shadow map的分辨率,而可以压缩到400个patch。
RSM技术通常被用来做游戏中的手电筒。
- Pros:易于实现
- Cons:
- 由于采用了shadow map,performance和光源数线性相关
- No visibility check for indirect illumination
- Many assumptions:diffuse reflectors,depth as distance, etc
- Sampling rate/ quality trade off
Light Propagation Volumes(LPV)
Key idea:Radiance travels in a straight line and does not change
Key solution:将空间划分为网格,从被光源直接照亮的物体表面出发,通过网格向各方向传播
具体步骤:
- 用和RSM一样的方法得到被光源直接照亮的点的集合,可以适当减少surface patch的数量
- 将点云作为虚拟光源注入到网格中
- Sum up directional radiance distribution in each grid cell
- 将和投影到二阶球谐函数上
- Volumetric radiance propagation
- For each grid cell, collect the radiance received from each of its 6 faces
- Sum up, and again use SH to represent
- Repeat this propagation several times till the volume becomes stable(差不多4到5次收敛)
- Scene lighting with final light propagation volume
- For any shading point, find the grid cell it is located in
- Grab the incident radiance in the grid cell(from all directions)
- shade
疑惑:grid cell是如何收集radiance的
- 如果是像cubemap一样收集,那岂不是不向grid中心的信息都丢失了?
- 如果是简单地相加,那不就相当于把各个面接收到的光的起点都移动到grid cell的中心,那光线就不是沿直线传播了呀?而且按照论文中的图示,感觉论文就是这样做的,不能理解。